The Equation of Motion
Vrebound = eA * Vinbound + (1+eA) * Vpaddle
Source: Characterizing the performance of baseball bats by Nathan
Determining eA
First, it's important to realize that eA takes on different values depending on the relative speed of the ball and paddle before impact. Second, eA is for a specific paddle and ball. Change the paddle or ball and eA changes.
The easiest way to determine eA is to shoot a ball at a stationary paddle and measure inbound and rebound velocity. This is equivalent to a blocked shot at the net. Since Vpaddle = 0, the equation can be rearranged to find eA as the ratio of rebound velocity and inbound velocity.
eA = Vrebound / Vinbound
The graph to the right is a plot of the inbound and rebound velocities for a Pulse V paddle using an X40 ball. It's important to note how strange the graph is. A shot from your opponent traveling toward you at 30 mph will rebound off your new Pulse V paddle at 12 mph. But a shot traveling twice as fast, 60 mph, will rebound of your paddle at just 7 mph?? Slower??
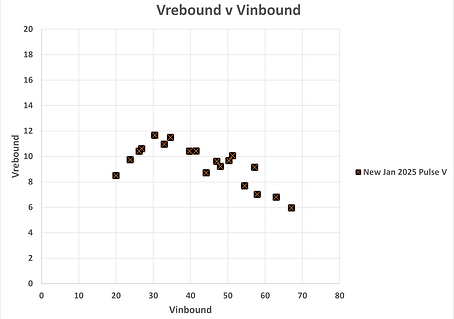

The effect is real and is caused by the ball deforming ("pancaking") and becoming much less efficient at returning energy (less bouncy) when it hits the paddle face at high speed.
In the technical literature this "efficiency" is called the collision efficiency (eA)
We can take the data from the graph above and plot collision efficiency eA vs Vinbound

The beauty of collision efficiency is that the rebound velocity from any combination of inbound velocity and paddle velocity can be calculated using this equation:
Vrebound = eA * Vinbound + (1+eA) * Vpaddle
Block
The data in the first graph above was collected by shooting a ball at a stationary paddle meaning Vpaddle = 0. This is the situation where a shot is blocked at the net. The equation simplifies to:
Vrebound = eA * Vinbound
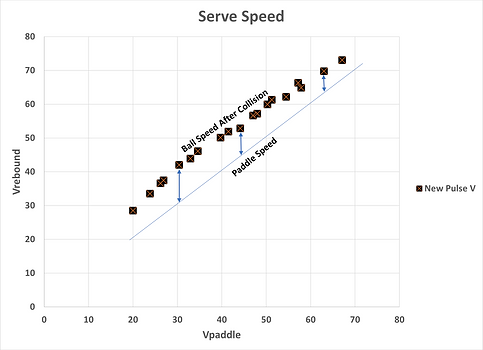
Serve
Now, let's examine the situation during a serve when Vinbound =0 and the paddle is moving over a range of velocities. The equation simplifies to:
Vrebound = (1+eA) * Vpaddle or
Vrebound = Vpaddle + eA * Vpaddle
The rebound velocity becomes the velocity of the paddle plus a "bump" from eA.
The graph of Vrebound during a serve is what might be expected - there is no fall off in rebound velocity.
What we do see is a bigger "bump" (bue arrows) above the paddle speed at 30 mph compared to the "bump" above the paddle speed at 60 mph.
Note: The graph to the right is a physics based representation of what is supposed to happen if a ball is served using a Pulse V paddle. To test the accuracy of the equation someone would have to build a machine that swings a Pulse V paddle at a stationary ball while measuring the paddle speed and the resultant ball speed.
Why are people shooting balls at paddles? The answer is that the rebound velocity can be calculated under a variety of conditions. One of those reasons is to limit paddle power. A serve at 50 mph - the test speed for UPA-A's PBCOR measurement - is important to measure paddle power. Another reason is for paddle reviewers to quantify power and pop so as to compare paddle performance.
Below are some examples using the equation:
Vrebound = eA * Vinbound + (1+eA) * Vpaddle.
The collision efficiency (eA) at 50 mph is about 0.2. A serve with a stationary ball and a 50 mph paddle swing would result in a 66.6 mph rebound velocity.
Vrebound = 0.2 * 0 + (1.2) * 50 = 60 mph
For a blocked shot at the net where the ball is traveling toward you at 50 mph the collision efficiency is again about 0.2 and the result is a 10 mph rebound velocity.
Vrebound = 0.2 * 50 + (1.2) * 0 = 10 mph
For a volley where the ball is traveling toward you at 25 mph and you are swinging the paddle at 25 mph (the relative velocity between ball and paddle is 50 mph) the collision efficiency is again about 0.2. The result is a ball traveling toward the opponent at 35 mph.
Vrebound = 0.2 * 25 + (1.2) * 25 = 35 mph
For a volley where the ball is traveling toward you at 15 mph and you are swinging the paddle at 15 mph, the relative velocity between ball and paddle is 30 mph. The collision efficiency is determined at 30 mph and is 0.35. The result would be a ball traveling toward the opponent at 25.5 mph.
Vrebound = 0.35 * 15 + (1.35) * 15 = 25.5 mph